Mohamadreza Ahmadi | Perception-Aware Autonomy

Emerging applications in autonomy require autonomous agents that can actively perceive or sense the uncertain environment and make decisions. Furthermore, the decision making method need to take into account communication constraints, while satisfying high-level mission specifications

For instance, in the upcoming Mars 2020 rover mission, a Mars rover is tasked to safely explore an uncertain environment and coordinate with a scouting helicopter. Since the energy supply of Mars rovers is limited (produced from a thermoelectric generator), the communication between the Mars rover and helicopter can result in further power consumption and reduce the lifetime of the rover. Missions of such sophisticated nature will necessitate on-board autonomy. Nonetheless, tight sensing constraints, due to the power consumption of on-board sensors and transmitters, and bandwidth limitation on data sent from the Earth and orbiting satellites further complicates the navigation task. In these cases, it is necessary for autonomous agents to make decisions to complete an specified task with optimal information cost involved for perception.

Artist’s rendering of the proposed helicopter to scout for the Mars rover. The helicopter can fly ahead and send information back to the rover about the presence of any obstacles. [Courtesy of NASA JPL]

Markov Decision Processes with Perception Costs

Markov decision processes (MDPs) are one of the most widely studied models for decision-making under uncertainty in the fields of artificial intelligence, robotics, and optimal control.

I model the interaction between an autonomous agent and an uncertain environment using an MDP. In order to account for the perception costs, I consider an additional cost term in terms of transfer entropy. We use the additional transfer entropy cost to quantify the directional information flow from the state of an MDP (representing the uncertain environment or the location of the autonomous agent) to the control policy. By minimizing the transfer entropy, I promote randomized policies that rely less on the knowledge of the current state of the system. I also consider high-level mission specifications that are defined in terms of linear temporal logic (LTL) formulae.

Let $\{\mathcal{X}_t\}_{t=0}^{T-1}$ and $\{\mathcal{U}_t\}_{t=0}^{T-1}$ be a finite set of states and actions, respectively, for an MDP and $X^T=\{X_1,\ldots,X_n\}$ , with upper case letters denoting random variables and lower case ones their instantiations. The transfer entropy is given by

$I({X}^{T-1}\rightarrow U^{T-1}\| {X}^{T-1})=\sum_{t=0}^{T-1} I({X}^t; U_t|U^{t-1},{X}^t).$

where the conditional mutual information $I ({X}^t;U_t \vert U^{t-1},{X}^{t})$ is described as

$I ({X}^t;U_t \vert U^{t-1},{X}^{t}) = \sum_{\mathcal{X}^t, \mathcal{U}^t} \mu_t(x^t, u^{t-1})\log\frac{q_t(u_t\vert x^t, u^{t-1})}{\sum_{\mathcal{X}^t}\mu_t({x}^t, u^{t-1})q_t(u_t\vert x^t,u^{t-1})},$

wherein, $q_t(u_t\vert x^t,u^{t-1})$ denotes the policy and $\mu_t(x^t, u^{t-1})$ is the joint states and actions distribution. Then, formally, I consider the following sequential decision making problem

$\begin{cases} \max\limits_{\{q_t\}_{t=0}^T} \mathbb{P}(x \models \varphi) \\ I({X}^{T-1}\rightarrow U^{T-1}\vert {X}^{T-1}) \le D_0, \end{cases}$

that is, maximizing the probability of satisfying the specification given by formula $\varphi$ given the sensing budget $D_0$ . Alternatively, I optimize the weighted sum of both the probability of satisfying the specifications and the transfer entropy term.

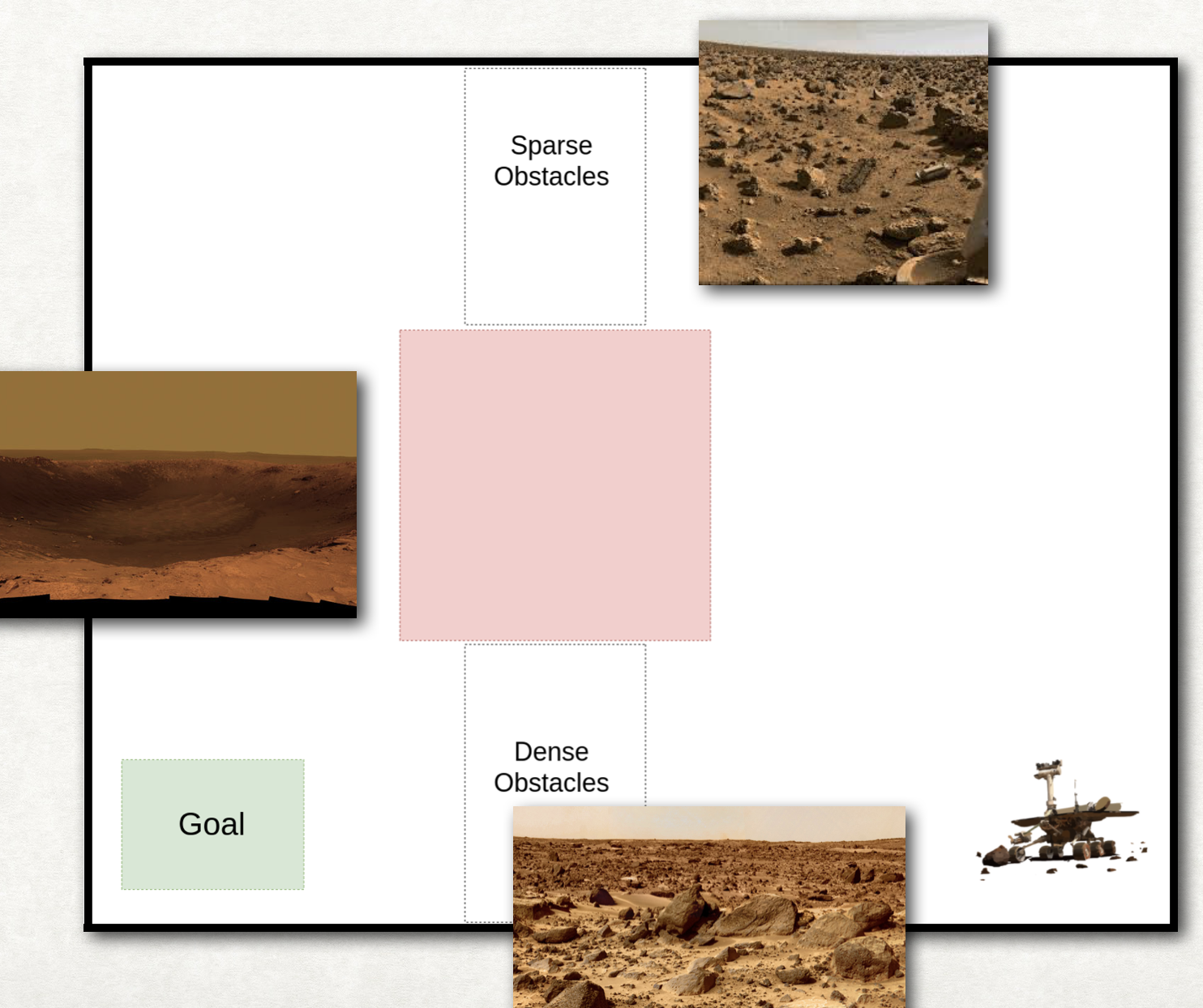
The figure below shows an example of sensing-aware autonomous navigation satisfying the LTL formula $\lnot$ ‘crash’ $\mathcal{U}$ ‘goal’ (do not hit the obstacles until you reach goal region).

Left: Mars rover navigation example. The red region is impassable terrain, e.g. a crater. There is a region with a high density of obstacles and one with a low density of obstacles. All other regions are assumed to be obstacle free. The regions with high density require more sensing; whereas, the region with sparse obstacles need less sensing effort. Center: Navigation with small weighting for perception. Right: Navigation with large weighting for perception. The rover goes through the sparse obstacles to incur less sensing cost.

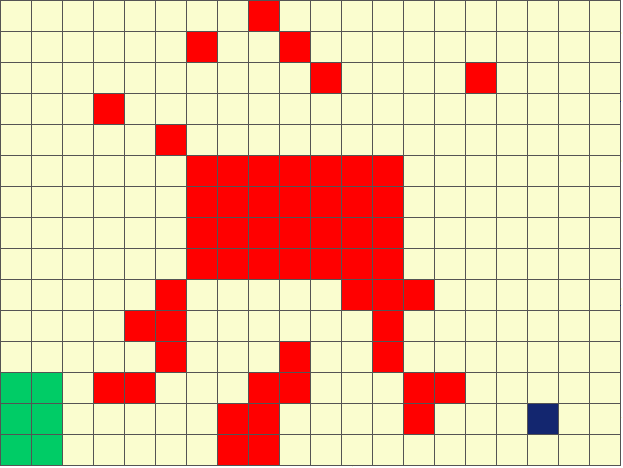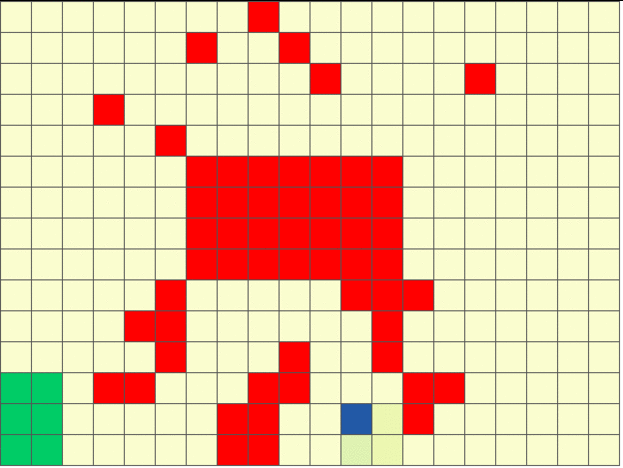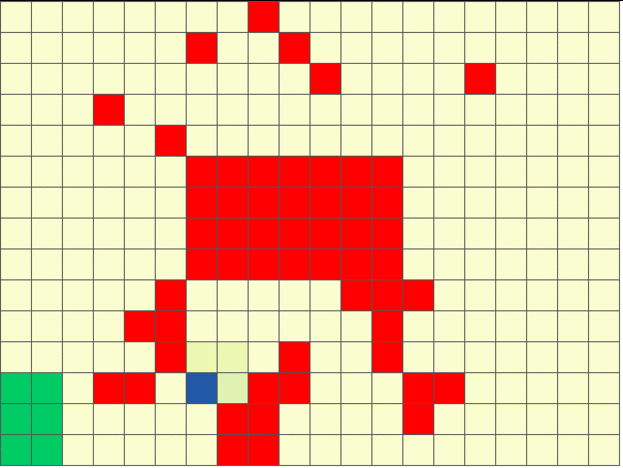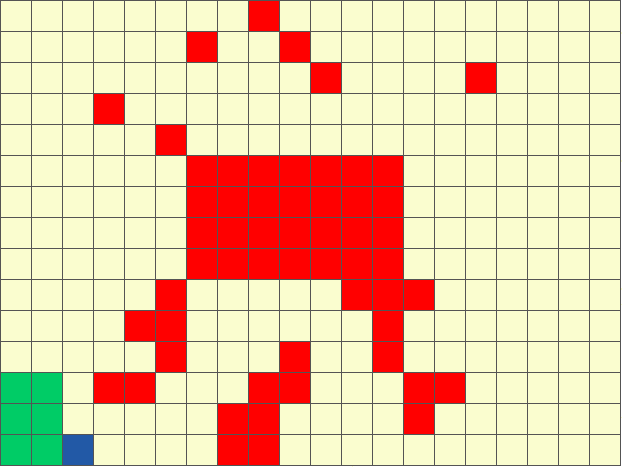
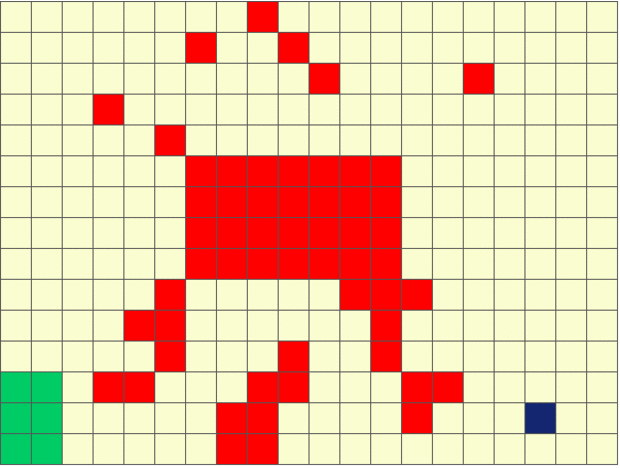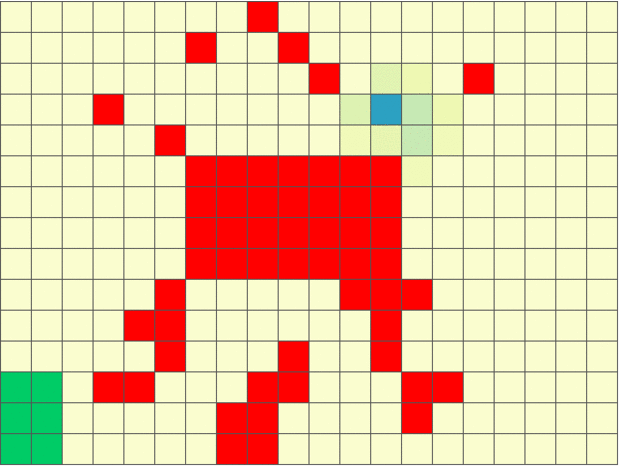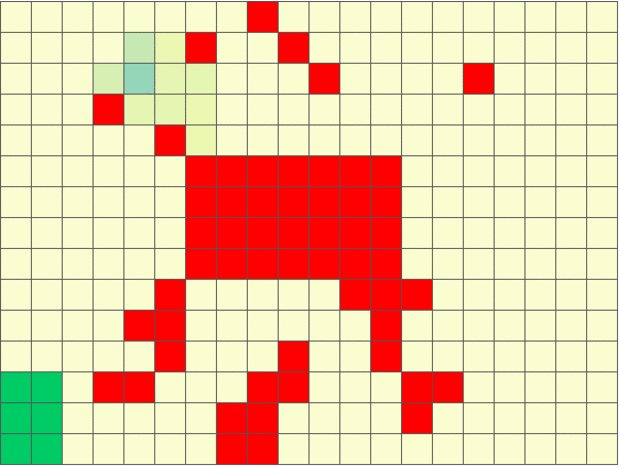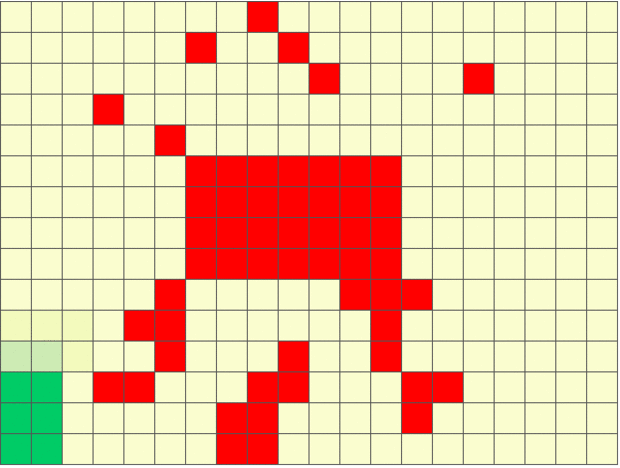
Stochastic Games with Perception Costs

Stochastic games, introduced by Shapely in 1953, are dynamic games over a sequence of stages with probabilistic transitions. At the beginning of each stage the game is in some state. The players select actions and each player receives a payoff that depends on the current state and the chosen actions. The game then moves to a new random state, whose distribution depends on the previous state and the actions chosen by the players. Stochastic games can be used to model and analyze discrete systems operating in an unknown (adversarial) environment. Applications of such games run the gamut of computer networks to economics.

However, in real-world games involving autonomous agents making decisions under uncertainty, the agents have a limited perception or information budget, since information acquisition, processing, and transmission are costly operations. In particular, in two-player uncertain adversarial environments, where one player enters the opponent’s territory, we seek a wining strategy with minimum sensing.

I considered finite two-player stochastic games, wherein in addition to the conventional cost over states and actions of each player, I included the perception budget in terms of transfer entropy. Formally, my goal was to find strategies $\{q_t^u\}_{t\in \mathcal{T}}$ and $\{q_t^w\}_{t\in \mathcal{T}}$ that solve the following class of dynamic stochastic games

$\min_{\{q_t^u\}_{t \in \mathcal{T}}} \max_{\{q_t^w\}_{t \in \mathcal{T}}} J(X^{T+1}, U^T,W^T) + \frac{1}{\gamma_1} I(X^T \to U^T) - \frac{1}{\gamma_2} I(X^T \to W^T),$

where $J(X^{T+1}, U^T,W^T) := \sum_{t\in \mathcal{T}} \mathbb{E}~c_t(X_t,U_t,W_t) + \mathbb{E}~c_{T+1}(X_{T+1})$ is the total payoff function, $I(X^T \to U^T)$ is the transfer entropy for the (good) player, $I(X^T \to U^T)$ is the transfer entropy for the adversary, and $\gamma_1,\gamma_2>0$ . In particular, I am interested in the case $\gamma_2 \to \infty$ , since I often assume the adversary has full access over its states.

I found a set of pure and mixed strategies for such a game via dynamic programming. The application of dynamic programming leads to a set of coupled nonlinear equations that I solve using the modified Arimoto-Blahut algorithm.

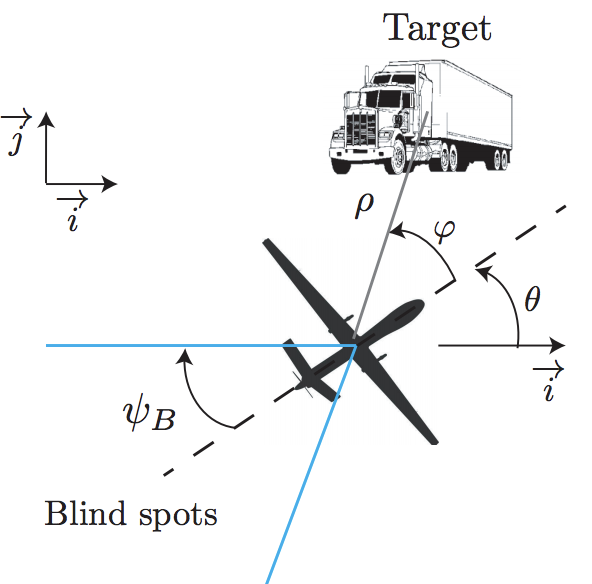
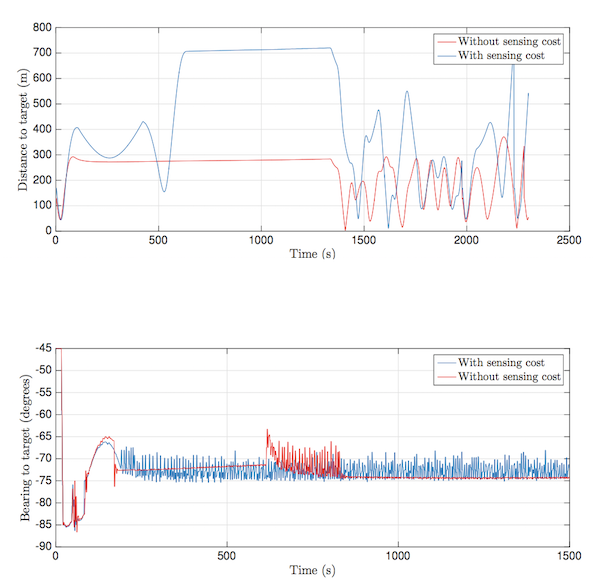
I considered a case study of a UAV vision-based target tracking task of an (evasive) ground vehicle using UAV simulation environment OpenAMASE developed at Air Force Research Laboratory. The goal of the UAV is to keep the adversarial ground vehicle in the field of view of its camera despite the evasive maneuvers of the ground vehicle.

Left: Schematic diagram of a UAV with a mounted camera. Center: Snapshot of simulation on AMASE. The purple and blue UAVs are tracking the green target ground vehicle. The purple UAV has no sensing cost. The corresponding colored polygons in front of the respective UAVs are the sensor footprint of the camera and the polygons behind the UAV represent the camera blindspots. Right: Graphs of distance and bearing from the UAVs to the target in both the without-perception-cost (in red) and with-perception cost (in blue) cases. In the presence of perception cost, the UAV typically maintains a larger distance from the target. This is because the target entering the blind spot of the gimbal mounted camera is penalized more heavily. Not getting too close to the target gives the UAV more time and space (the target has a faster turn rate) to react to the target when it is maneuvering towards the blind spot.