Control-Oriented Learning
In several control and robotics applications, a mathematical model of the system is not available a priori. Conventional techniques in machine learning and system identification rely on collecting large sums of data to construct a model or to achieve control performance. However, in many cases, especially in aerospace applications, collecting data is exorbitantly costly, especially, in aircraft failure scenarios. Due to the safety-critical nature of these systems, we are interested in control and learning methods that can guarantee safety, optimality, and performance using on-the-fly learning from the scarce data.
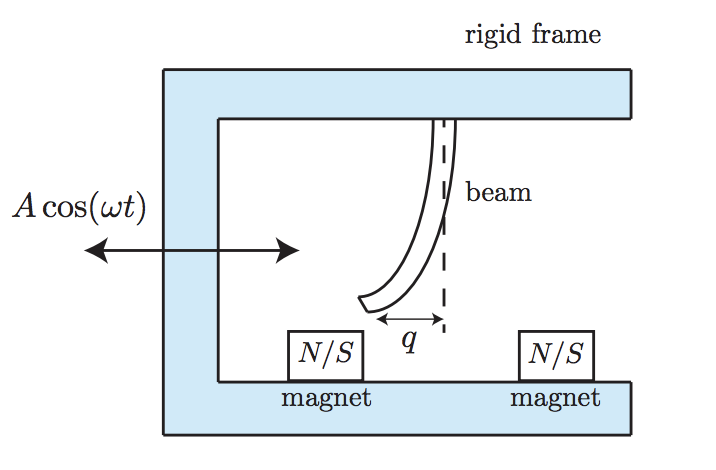
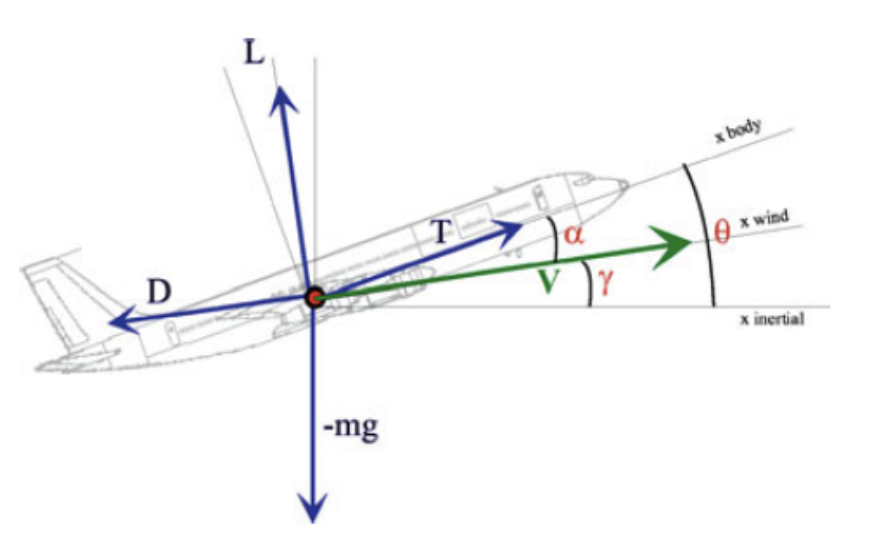
Even if a mathematical model of system is not available, we often have some knowledge or side information. The side information can be in terms of “system-theory” estimates, e.g. integral-quadratic-constraints (IQCs), or based on the physics of the system or the environment. For example, a flying aircraft with wing failure should follow the laws of aerodynamics.
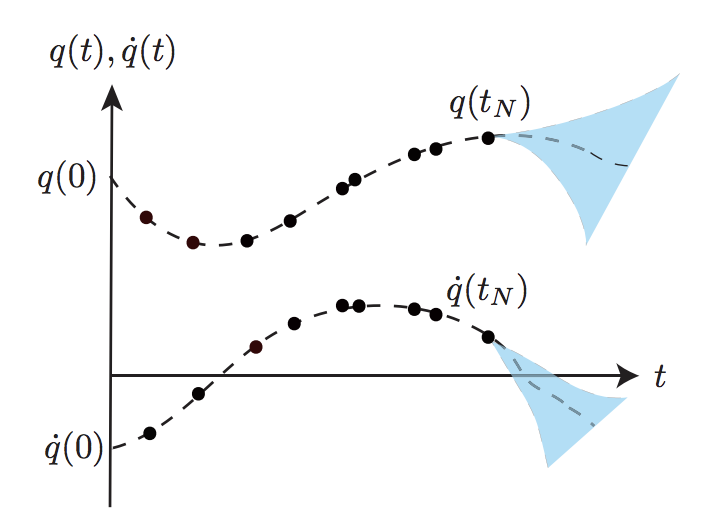
We proposed techniques that take advantage of the side information and learn physically-viable models of the system from scarce data obtained from a single trajectory. These methods provide bounds on error growth and can be used for safety control.
We proposed techniques that take advantage of the side information and learn physically-viable models of the system from scarce data obtained from a single trajectory. These methods provide bounds on error growth and can be used for safety control.
Interpolation-Based Methods
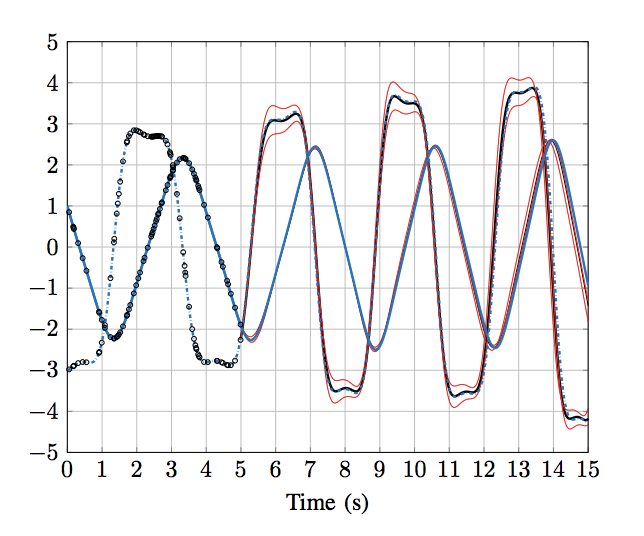
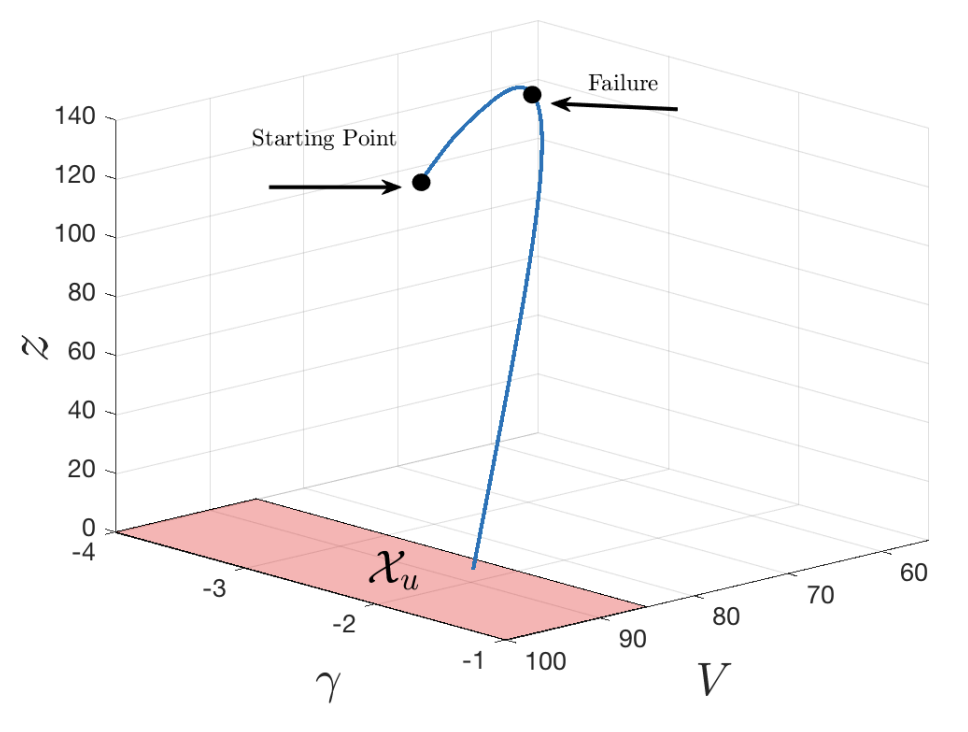
We considered safety assessment of systems for which scarce data (by scarce, we imply that the number of observations is not large enough for determining the complete dynamics using a system identification or a machine learning method) is available. To this end, motivated by the recent works on Whitney’s extension problem, we proposed a data-driven differential inclusion model of the system based on the piecewise-polynomial approximation of the state data and some regularity side information on the evolution of system state, e.g. maximum velocity or acceleration.
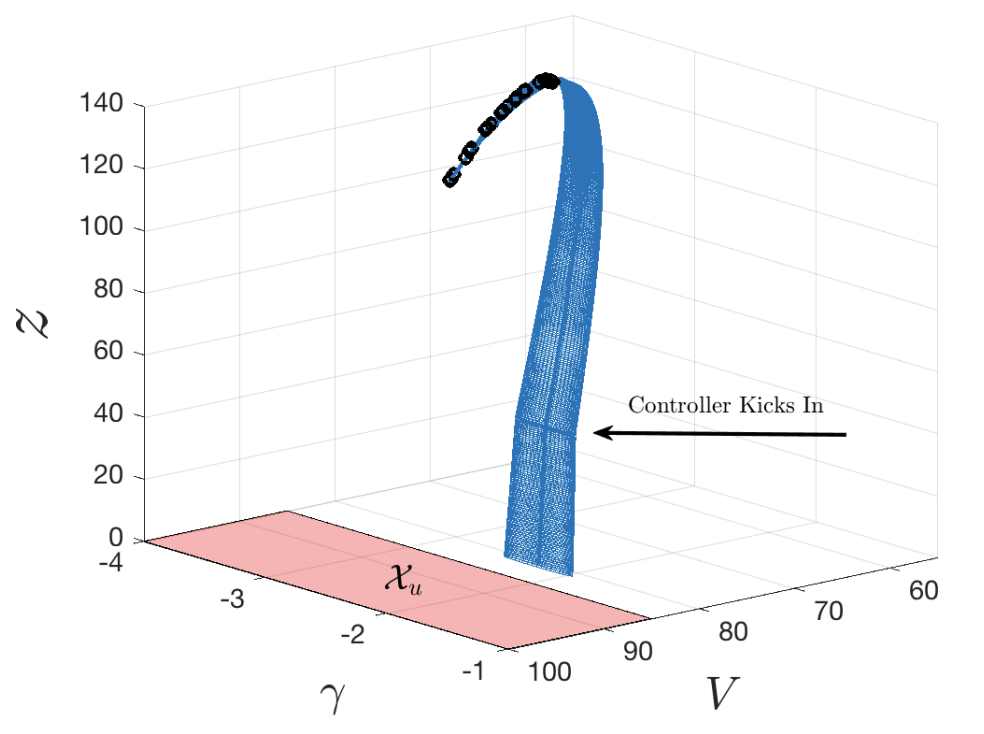
Equipped with this data-driven model, we formulated a safety assessment theorem based on barrier certificates for differential inclusions. The barrier certificates were then computed using semi-definite programming. The extension of this work was developed, which can take advantage of more side information in terms of conservation laws, symmetries and integral quadratic constraints. We also synthesized controllers that can ensure safety and optimality based on the data-driven models.
Lagrangian/Hamiltonian-Based (Physics-Based) Methods
I formulated a method based on quadratic programming to approximate the Lagrangian or the Hamiltonian of a system from scarce data from a single trajectory. The proposed approach is not data hungry and, due to its quadratic programming formulation, scale very well with the the number of states. If some a priori knowledge about the symmetries is available, I showed that it can be added as a set of linear constraints to the quadratic programs. I further demonstrated how the approximation errors can be bounded and used to construct data-driven differential inclusions that can be used for control purposes.