Mohamadreza Ahmadi | Convex Methods for PDEs

The need for accurate models to study complex dynamical systems has driven research efforts towards partial differential equations (PDEs)- equations involving derivatives with respect to more than one independent variable. Many, seemingly distinct, physical phenomena running the gamut of quantum systems to fluid mechanics can be mathematically formalized by PDEs.

Despite this unique modeling paradigm, the analysis and control problems of PDEs are fettered by several complications: in PDEs, the solution (state) is a function of both space and time; the solution belongs to an infinite-dimensional (function) space, as opposed to a Euclidean space in the case of ordinary differential equations (ODEs); unlike Euclidean spaces, for function spaces, say Sobolev spaces, different norms are not equivalent. Therefore, stability and input-to-state/output properties of PDEs differ from one norm to another. Due to the latter difficulties, most available analysis methods for PDEs (especially, nonlinear PDEs) rely on ad hoc (pen and paper) analytical methods rather than algorithmic and computational ones.

In my DPhil research at the University of Oxford, funded by a Clarendon Scholarship and the Sloane-Robinson Scholarship, I laid a theoretical foundation based on convex optimization for the analysis of a large class of nonlinear PDEs.

In my DPhil research…I laid a theoretical foundation based on convex optimization for the analysis of a large class of nonlinear PDEs.

Convex Methods for Solving Integral Inequalities

Stability analysis, input-output analysis and controller synthesis problems of systems described by PDEs can be often reduced to checking the positivity of a set of integral inequalities subject to boundary conditions. The key tool in conventional (analytical) methods for verifying the positivity of these integral inequalities is integration-by-parts. Application of functional inequalities, such as Wirtinger inequality, Poincare inequality, and the Sobolev Embedding Theorem is also required.

I proposed a methodology that converts the problem of checking the positivity of integral inequalities, subject to a set of boundary conditions, into checking a set of sum-of-squares programs. That is, the following optimization problem

$\begin{cases} \min\limits_{u\in \mathbb{R}^n} c^T u \\ a_{k,0}(x)+a_{k,1}(x)u_1+\cdots+a_{k,n}(x)u_n \text{ is sum-of-squares },~k=1,\ldots,N_s, \end{cases}$

where $c \in \mathbb{R}^n$ , polynomials $\{ a_{k,j} \}$ are given, and $u \in \mathbb{R}^n$ are variables. Sum-of-squares programs can be solved efficiently using tools such as SOSTOOLS. The method I introduced is based on a quadratic representation of integral inequalities and automating integration by parts for one dimensional and two dimensional spatial domains.

I proposed a methodology that converts the problem of checking the positivity of integral inequalities, subject to a set of boundary conditions, into checking a set of sum-of-squares programs.

The table below illustrates the method proposed in my dissertation and compares it with quadratic inequalities and polynomial inequalities. The first row describes the original inequality to be checked and the second row presents the solution based on convex optimization. The last column “Integral Quadratic Inequality” pertains to my proposed method.

Quadratic Inequality	Polynomial Inequality	Integral Quadratic Inequality
$x^T M x \ge 0,$	$\zeta[x]^T \bar{M} \zeta[x] \ge 0,$	$\begin{cases} \int_\Omega \left(D^\alpha u(\theta) \right)^T \tilde{M}(\theta) D^\alpha u(\theta)~\mathrm{d}\theta \ge 0, \\ B D^{\alpha-1}u \mid_{\partial \Omega} = 0, \end{cases}$
$M \succeq 0.$	$\begin{cases} \bar{M} + G \succeq 0\\ \left\{ G \mid \zeta[x]^T G \zeta[x]=0 \right\}. \end{cases}$	$\begin{cases} \tilde{M}(\theta)+H(\theta) \succeq 0,~\forall \theta \in \Omega, \\ \left\{ H(\theta) \mid \int_\Omega \left(D^\alpha u(\theta) \right)^T {H}(\theta) D^\alpha u(\theta)~\mathrm{d}\theta = 0 \right\}. \end{cases}$

Stability and Dissipativity Analysis of PDEs

Equipped with this computational framework, I formulated algorithmic methods for stability analysis, input-output analysis, and safety verification of systems described by PDEs, which can all be implemented based on convex optimization. For input-output analysis, I proposed a framework based on dissipation inequalities for PDEs to study passivity, reachability, induced input-output norm boundedness, and input-to-state stability (ISS). I considered both cases of in-domain and boundary inputs and outputs. I also proposed a compositional analysis method for interconnections of PDEs using small gain conditions.

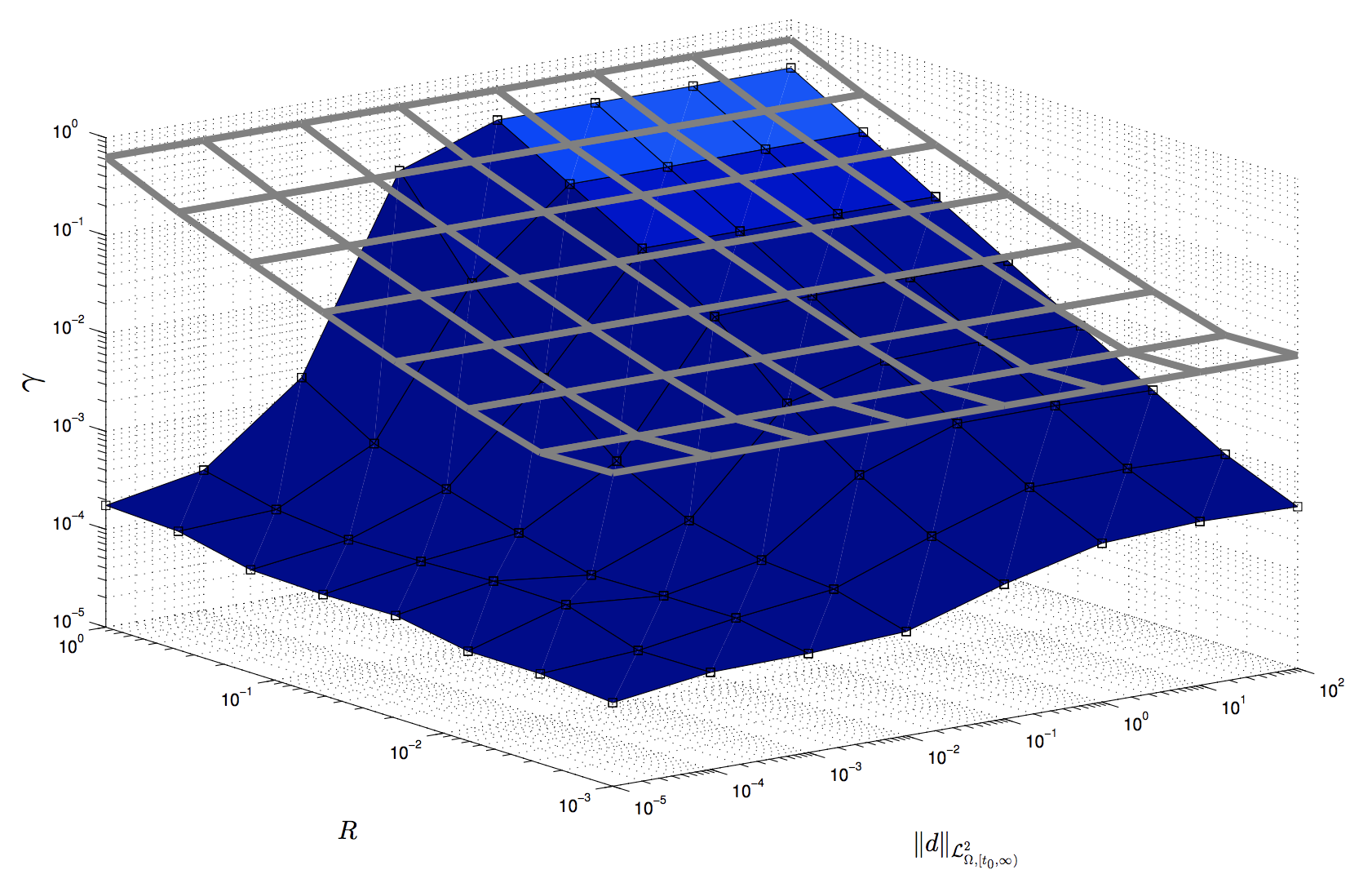
For example, the figure below demonstrates the (nonlinear) induced $L_2$ -to- $L_2$ norm from the in-domain inputs $d(t,x)$ to the states $u(t,x)$ of the Burgers’ equation

$\begin{cases} \frac{\partial u}{\partial t} = \frac{1}{R}\frac{\partial^2 u}{\partial x^2}-u \frac{\partial u}{\partial x}+d, \quad x \in [0,1],~t>0, \\ \text{subject to boundary conditions }u(t,0)=u(t,1)=d(t,0)=d(t,0)=0, \end{cases}$

obtained using my proposed method.

The induced norm surface in terms of parameter R and the norm of the input. The gray net illustrates the induced norms obtained using the energy functional and the blue surface represents the induced norms obtained using the storage functional computed via convex optimization. The results obtained using my method can capture the nonlinear behavior of the input-output norm for the Burgers' equation, i.e., the induced norm changes nonlinearly with different values of the input norm (a behavior well-known in nonlinear systems). The results obtained based on the energy functional (the traditional storage functional candidate), on the other hand, provide conservative upper bounds to the actual norm of the nonlinear system.

Safety Verification of PDEs

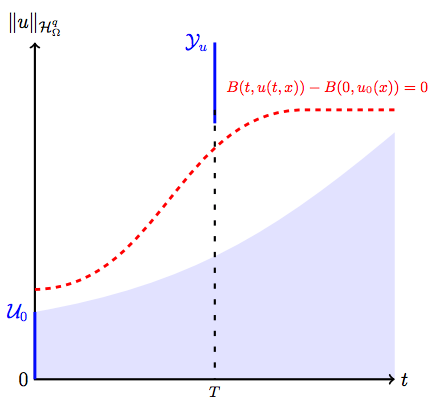
For safety verification, i.e., the problem of checking whether the solutions of the PDE satisfy a set of constraints at a particular point in time, I proposed a method based on an extension of barrier certificates to infinite-dimensional systems. In this respect, I introduced barrier functionals, which are functionals of states of a PDE. Given a set of initial conditions and an unsafe set, I demonstrated that if such a functional exists satisfying two (integral) inequalities, then the solutions of the system do not enter the unsafe set. Therefore, the proposed method does not require finite-dimensional approximations of the PDE or domain discretization as is the case in conventional methods.

The figure below illustrates the use of barrier functionals for predicting the behavior of PDE solutions: any solution $u(t, x)$ with $u(0, x) \in \mathcal{U}_0$ (depicted by the shaded area) satisfies $u(T, x) \in \mathcal{Y}_u$ . Thus, the system is $\mathcal{Y}_u$ -safe at time $t = T$ but not for $\forall t > 0$ . Note that the zero-level set of the barrier functional separates the set of evolutions from the unsafe set at time $t=T$ .

Illustration of a barrier functional for a PDE system.

The method also has direct applications in bounding functional outputs of PDEs, e.g., bounding the drag and lift forces of an airfoil surrounded by flow. Moreover, the barrier functionals method was used to propose a methodology based on convex optimization to bound moment functionals of nonlinear stochastic differential equations through the Feynman-Kac PDE.

I formulated algorithmic methods for stability analysis, input-output analysis, and safety verification of systems described by PDEs, which can all be implemented based on convex optimization.

Applications in Fluid Dynamics:

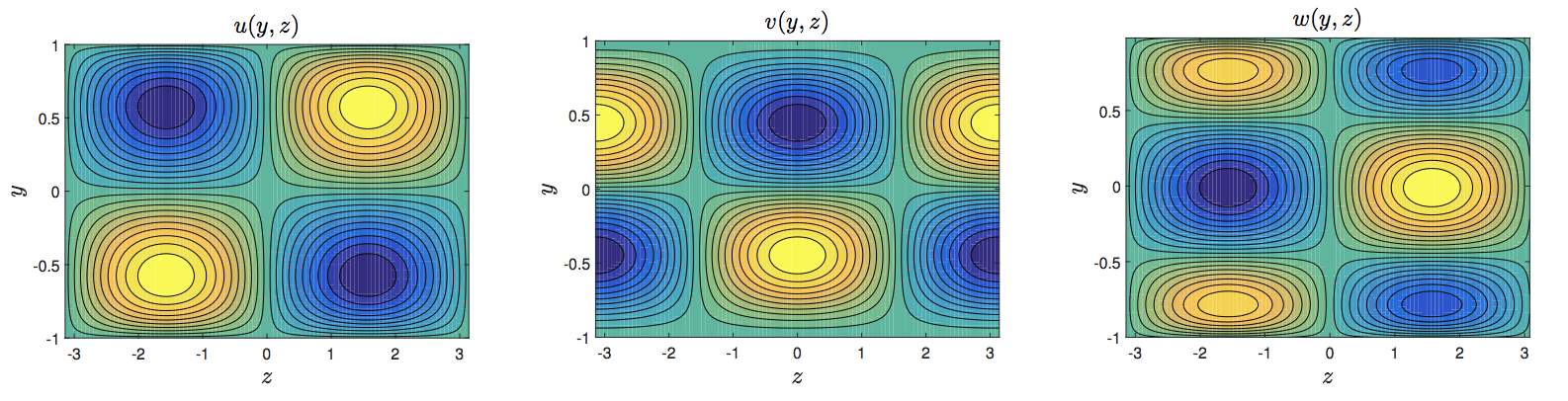
Hydrodynamic stability is a well-studied field of fluid dynamics, aiming in understanding the stability properties of fluid flows and in particular when these become unstable. The methods usually employed involve linearization of the equations around a base flow solution, followed by numerical analysis revealing the Reynolds number estimate for when this solution becomes unstable. Akin to the stability problem is the input-output analysis problem of fluid flows as underscored as early as Reynolds. These methods, however, have not been very promising to address issues for nonlinear flows. Indeed, there is a significant gap between the theoretical instability bounds and the onset of turbulence observed in experiments.

I proposed a framework based on dissipativity theory to understand input-output amplification properties of nonlinear PDE models of wall-bounded shear flows… My method can be applied to both channel flows and pipe flows, and is numerically implemented as the solution to a convex optimization problem.

I proposed a framework based on dissipativity theory to understand input-output amplification properties of nonlinear PDE models of wall-bounded shear flows, which are subject to invariant perturbations in one spatial coordinate, e.g., streamwise-constant plane Couette flows. In particular, I considered flows subject to body and other forcings, for which I study the input-output properties, including energy growth (transient growth for linear flows), worst-case disturbance amplification (induced $L_2$ -norms), and stability to persistent disturbances (ISS). My method can be applied to both channel flows and pipe flows, and is numerically implemented as the solution to a convex optimization problem, that can be solved efficiently using available computer software. I applied this method to a number of traditional flows, such as Taylor-Couette flow, plane Couette flow, Poiseuille flow, and Hagen-Poiseuille flow, revealing a correspondence between the stability bounds to persistent forcings and the (enigmatic) experimental estimates for transition to turbulence. This was the first time ISS was studied for fluid flows and my results provide a theoretical framework to predict the onset of turbulence in fluid flows.

This was the first time ISS was studied for fluid flows and my results provide a theoretical framework to predict the onset of turbulence in fluid flows.

The (culprit) perturbation flow structures for plane Poiseuille flow with maximum ISS amplification at Reynolds number 1855, leading to turbulence.